Predpostavimo, da imamo 4 igralce: A, B, C in D. Busmaster (A) najprej odpre prvo karto, in začne odštevati od 5.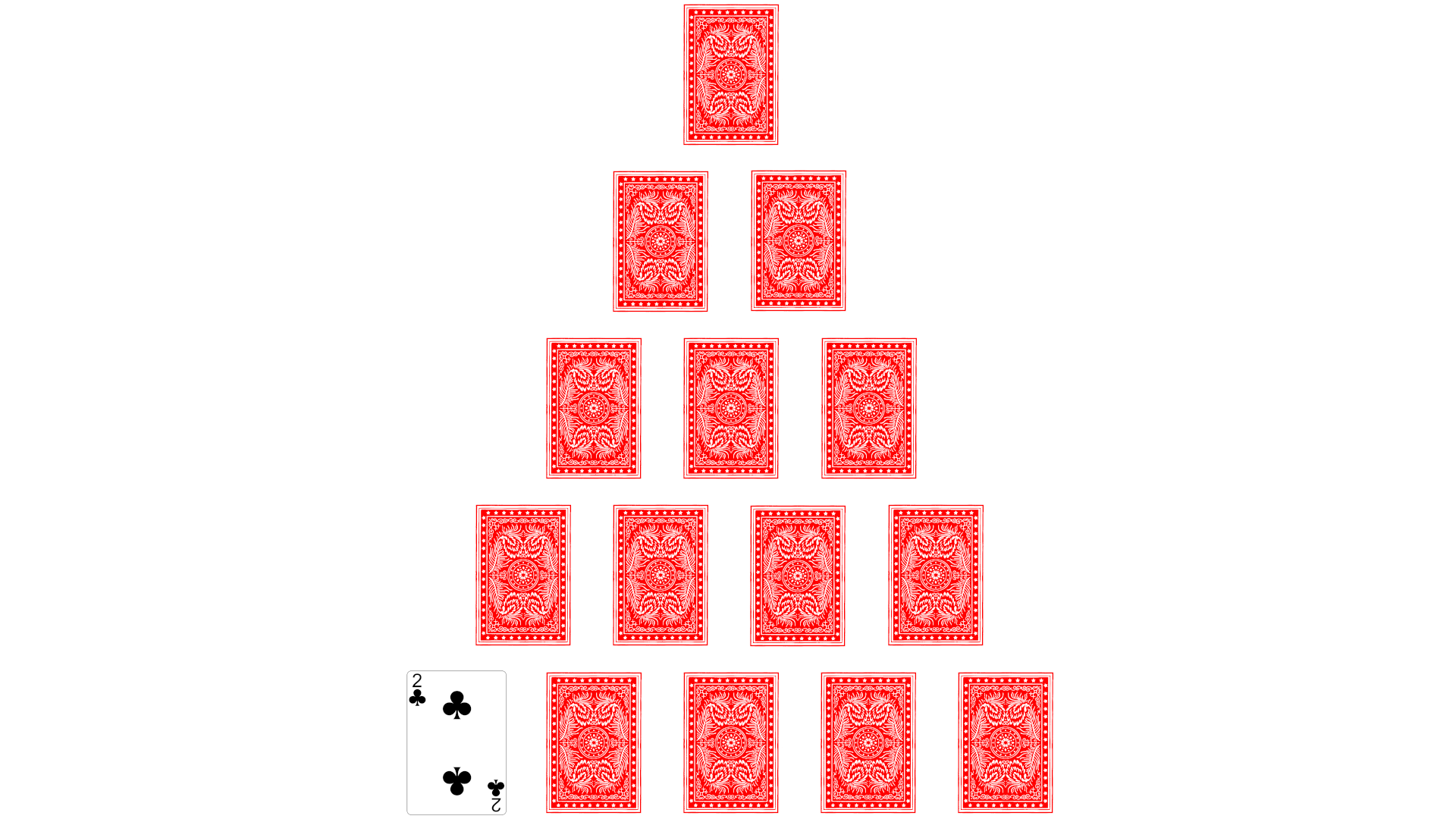 
Igralec B nato odloži srčevo 2, zaradi česar busmaster preneha z odštevanjem. 
Ker je igralec B odložil zadnjo (in edino) karto, lahko dodeli 1 požirek enemu od igralcev (razloženo v poglavju računanje požirkov). Recimo, da igralec B požirek dodeli igralcu C. Igralec C vzdigne kozarec, da bi naredil požirek, vendar preden se z kozarcem takne ustnic, igralec C odloži novo karto: pikovo 2. 
Kljub temu, da je pred kratkim igralec B naročil požirek igralcu C, se ta ukaz nemudoma razveljavi, in igralcu C ni treba narediti požirka (razen če mu ga igralec D ponovno dodeli). Sedaj ima igralec D (ki je odložil zadnjo karto), na voljo 2 požirka za dodelitev. Odloči se dodelitvi enega požirka igralcu B, in enega igralcu A (lahko bi tudi oba dodelil le enemu igralcu). Ko se katerikoli od izbranih igralcev z pločevinko/kozarcem dotakne ustnic, nihče ne more več dodajati kart na trenutno karto. Trenutna "runda" je zaključena, in nadaljuje se na naslednjo karto.
Pivska igra avtobus (piramida)
Avtobus (občasno znan tudi kot piramida) je popularna pivska igra, kjer igralci odkrivajo karte piramide in ostalim dodeljujejo požirke pijače glede na različne faktorje. Cilj te spletne strani je standardizacija in specifikacija pravil igre, saj se le-ta lahko bistveno razlikujejo od igralca do igralca. To stran lahko uporabite kot referenčna pravila v primeru nesporazuma o specifikah, ali kot navodila igre.
Na začetku se poljubno število igralcev posede za mizo. Skupaj določijo enega igralca, ki bo "busmaster". Ta igralec še vedno lahko igra igro, vendar je poleg tega zadolžen še za ostale stvari, ki so predstavljene na tej strani. Busmaster postavi trikotnik (piramido) iz premešanega kupčka navadnih igralnih kart, katere so obrnjene z hrbtno stranjo navzgor, kot prikazuje spodnja slika:
V navodilih predpostavljamo, da bo piramida visoka 5 kart, vendar je višina poljubna. V primeru večjega števila igralcev, je višino piramide smiselno povečati.
Po postavljeni piramidi busmaster nato razdeli karte igralcem. Število kart, ki jih dobi vsak igralec je enako višini piramide (pri standardni piramidi višine 5 torej vsi igralci dobijo 5 kart)
Ko je piramida enkrat postavljena in so karte razdeljene med igralce, se igra lahko prične. Busmaster začne postopoma odkrivati karte piramide od najnižjega nivoja naprej, od leve proti desni. Vizualizacija:
Ko busmaster odpre karto, začne odštevati od 5. Igralci lahko ustrezne karte na mizo odlagajo dokler busmaster ne odšteje do 0.
Katere karte so ustrezne?
Pri tej igri je relevantna le številka karte. Npr: če je odkrita križeva 2 (kot na sliki), lahko nanjo položimo katerokoli karto s številko 2, ne glede na barvo/simbol. Edina izjema je joker, katerega lahko položimo na katerokoli karto, vendar ga je zato smiselno varčevati za bližje koncu igre, iz razlogov do katerih še pridemo
Če ni bilo odložene nobene karte, ko busmaster prešteje do 0, enostavno nadaljujemo z naslednjo karto. V primeru, da so bile karte odložene pa igralec, ki je zadnji odložil karto razdeli požirke med preostale igralce, po pravilih katere bomo razložili v naslednjem poglavju. Pomembno: Ko prvi igralec položi karto, lahko busmaster preneha odštevati. Od te točke naprej lahko preostali igralci še vedno polagajo karte na kup, dokler se eden od igralcev, kateremu je bilo dodeljeno pitje, ne takne ustnic z pločevinko/kozarcem (tudi če je preminulo že >5 sekund). V naslednjih primerih:
- Igralčeva karta se dotakne mize, ko je busmaster že odštel do 0
- Igralec položi karto, ko je igralec, kateremu so bili dodeljeni požirkim že naredil požirek
- Igralec položi neustrezno karto
Pa mora igralec, ki je storil napako, za kazen spiti vse požirke, katerih so preostali igralci oproščeni.
Število požirkov, ki jih ima za dodeljevanje na voljo igralec, ki je zadnji položil karto, je odvisna od števila kart ter trenutnim nivojem piramide. Formula za izračun: p=k*i, kjer je p = števio požirkov, k = številu kart na kupu (brez originalne) ter i = trenutni nivo piramide. Edina izjema je zadnji nivo, kjer je faktor množenja = 2*h, kjer je h = višina piramide! Npr. pri standardni igri, z piramido višine 5, je ta faktor 10.
Igralec, ki deli požirke, jih med igralce lahko razdeli poljubno. Lahko da vse požirke enemu igralcu, lahko vsakemu enega, ali pa kombinira x požirkov enemu igralcu, y drugemu, z tretjemu itd. Pomembno je samo to, da je seštevek požirkov enak izračunanem številu.
Igralec, kateremu je bilo dodeljeno število požirkov, ki je večje od 10, se lahko odloči, da skupine po 10 požirkov zamenja za shote 0.03L žgane pijače (40% alk.). Npr. 20 požirkov lahko zamenja za 2 shota.
Ko je enkrat določen igralec, ki gre na avtobus, busmaster ponovno zmeša kupček kart, in jih 5 odkritih postavi v horizontalno vrsto, kot prikazuje spodnja slika.
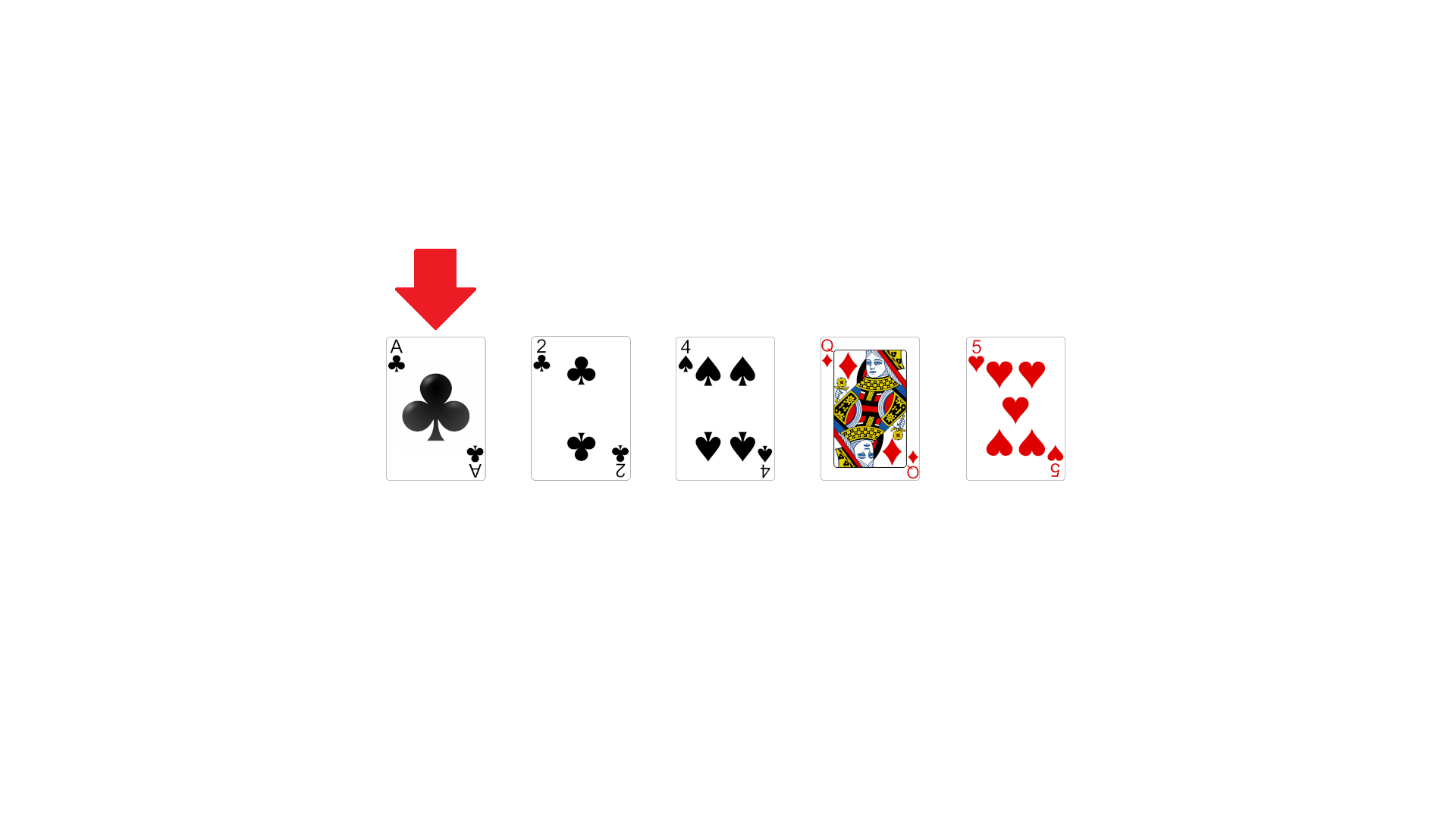
Igralec začne na skrajno levi karti, in se premika proti desni. Pri vsaki karti busmaster igralca vpraša, če meni da bo karta, katero bo na slepo vlekel iz vrha kupa, višja ali nižja od trenutne karte. Če igralec ugane pravilno, nadaljuje naprej na naslednjo karto, kjer ponovno ugiba. Če pa se igralec zmoti, pa ponovno začne na prvi karti na skrajno levi, in spije število požirkov, ki je enako "globini" avtobusa (v prvi rundi, ko je na mizi 5 kart, je to globina 1) zmnoženi z zaporednim številom kart, na kateri se je zmotil. Če se igralec vrne na začetek se od tam naprej upošteva zadnja karta na vrhu "kupa", in ne ponovno originalna karta. V primeru, da je izvlečena karta istega števila kot karta pod njo, se igralec lahko ponovno odloči za višje/nižje, medtem ko busmaster povleče naslednjo karto. Tako kot pri prejšnji fazi igre, tudi tukaj velja, da je 2 najnižja karta, joker pa najvišja.
Ko igralec uspešno prispe do konca vrste in pravilno ugane peto karto, busmaster ponovno postavi avtobus, le da tokrat z eno kart manj. Ta proces ponavljajte, dokler na mizi ni le ena karta, in jo igralec pravilno ugane. Tako kot pri piramidi, je tudi na avtobusu število požirkov odvisno od globine avtobusa:
- 1. nivo (5 kart) - faktor x1
- 2. nivo (4 karte) - faktor x2
- ...
Tako kot pri piramidi višine 5, je tudi na avtobusu faktor množitve pri zadnji globini (5. nivo oz. 1 karta) enak x10. Igralec lahko tudi na avtobusu skupine po 10 požirkov menja za shote
Busmaster najprej postavi avtobus z 5 kartami in igralec začne na skrajno levi karti (označeno z puščico).
Igralec na prvi karti (as) reče, da bo karta, ki jo bo izvelekel busmaster nižja od trenutne karte. Izkaže se, da je bila karta "junc", zato nadaljuje na naslednjo karto, kjer igralec predvideva, da bo višja. Izvlečena karta je 9, in ker je višja od 2, prav tako nadaljuje na naslednjo karto. Nato igralec ponovno pravilno ugane višje, in nadaljuje na kraljico. Na kraljici igralec ugane nižje, vendar je položena karta kralj. Posledično, se igralec vrne nazaj na prvo karto in spije 4 požirke.
Ko se igralec vrne na prvo karto, se za primerjave začne uporabljati karto na vrhu. Igralec ugane nižje, in ker je 4 nižje od junca, nadaljuje na naslednjo karto. Igralec ugane nižje, vendar ker je 10 višja od 9, igralec spije 2 požirka in se vrne na prvo karto.
Igralec pri prvi karti (4) ugane višje, in se posledično premakne na naslednjo karto. Od tam naprej pravilno predvideva vse karte, vključno z zadnjo (kralj višji od 5).
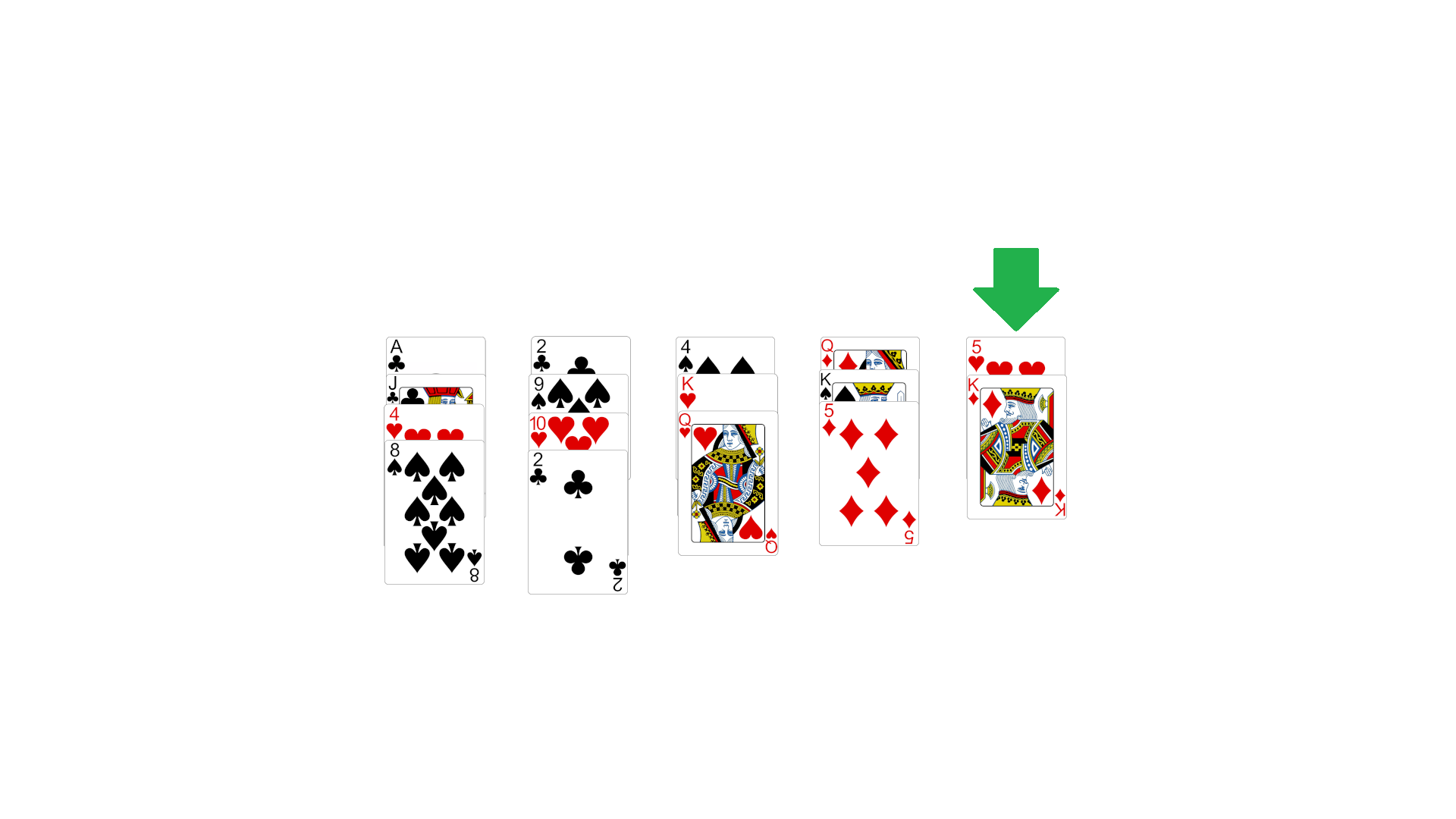
Busmaster karte pospravi, premeša in pripravi naslednji krog, kjer so le 4 karte, vendar je faktor množitve sedaj x2.
Pri prvi karti igralec ugane višje, in ker je 5 višja od 2, se premakne na naslednjo karto. Igralec ponovno ugane višje, 10 je višja od 5, spet se premakne naprej. Pri kralju igralec ugane višje, vendar ker je izvlečen as, se igralec vrne na prvo karto (sedaj bo to 5), in spije 6 požirkov.
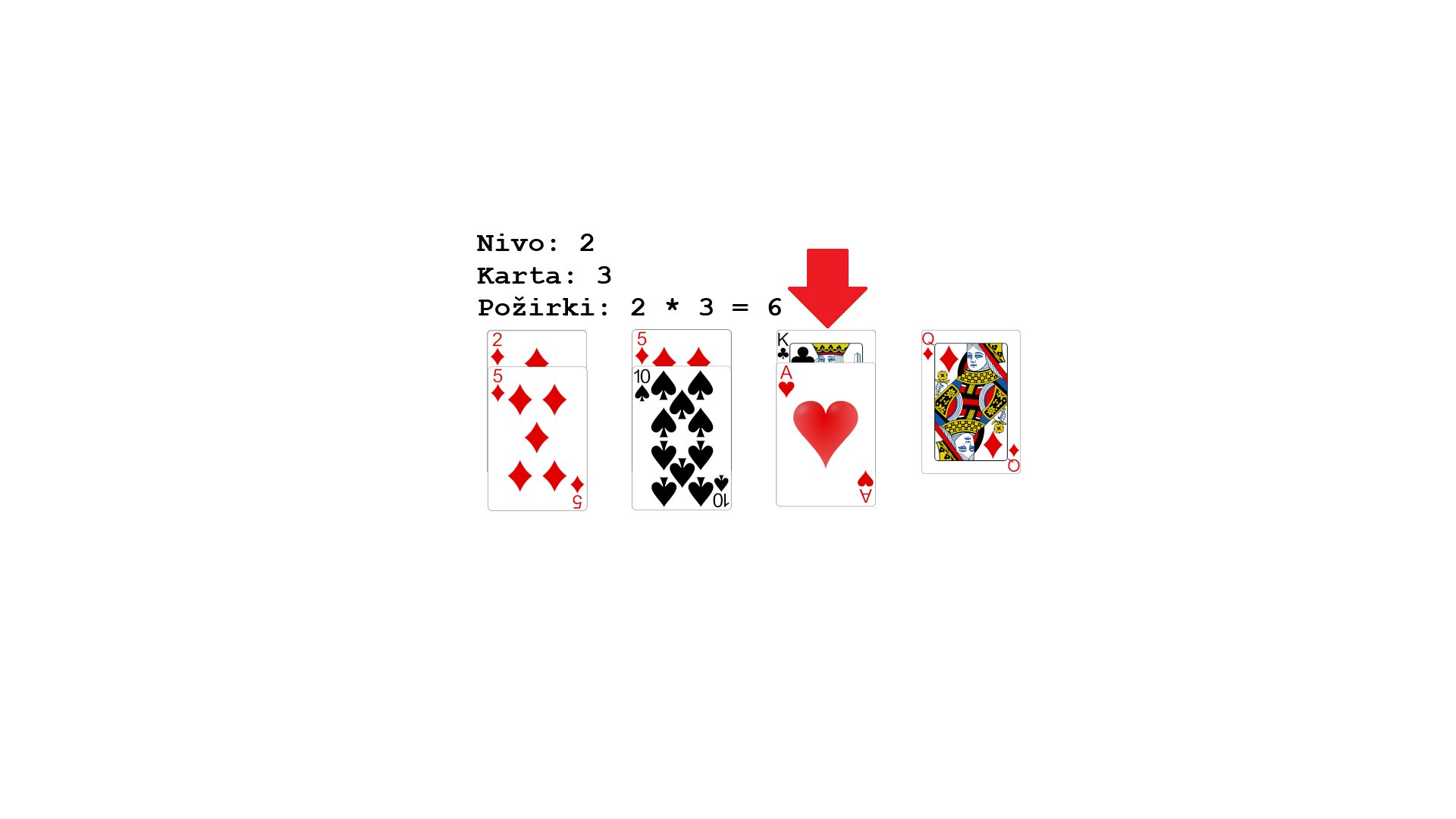
Igra se tako nadaljuje naprej. V naslednjem krogu so postavljene le 3 karte, vendar je faktor množenja x3 itd. Tako kot pri piramidi, je tudi pri avtobusu na koncu, ko je v vrsti le ena karta, faktor množenja x10